Cleyson007 escreveu:Bielto, pelo que entendi é o seguinte:
Para se ter o resultado de 7^-8 devemos ter (1/7)^7 no denominador.
Cleyson007 escreveu:Não vejo erro na resposta
Acredito que há um erro em seu gabarito.
Cleyson007 escreveu:Bielto, não há erro em sua resolução!
Para você encontrar a resposta do gabarito deverá ter no denominador. Daí, suponho que não seja um sétimo elevado a -7, mas
Abraço,
Cleyson007
![\[\frac{1}{7}^-^7\] \[\frac{1}{7}^-^7\]](/latexrender/pictures/f7c8bf703481ccf8bc3097f121d6f660.png) e não
e não ![\[7^-^7\] \[7^-^7\]](/latexrender/pictures/6ff979f4933e6554c2809f4c41bdcc63.png)
![\[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\] \[2^9^8+2^9^8.2^2-2^9^8.2^4 = 2^9^8(2^2-2^4) = -12\]](/latexrender/pictures/b19ff1fbcff57dc14c378eee52ef226f.png)
Russman escreveu:Fatore ono numerador e no denominador da fração.
![\[-\frac{12}{6}\] \[-\frac{12}{6}\]](/latexrender/pictures/9690d337a5e4522118adb92960c0d2a2.png)
![\[-\frac{11}{6}\] \[-\frac{11}{6}\]](/latexrender/pictures/4f15d97d803bcaf12871bbf3abd436b2.png)
 e
e 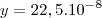 É correto afirmar que:
É correto afirmar que: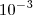 ou o correto é
ou o correto é 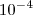 ? b)
? b) 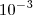 ou
ou 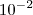 ? c)
? c) 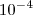 ou
ou 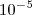
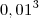 é:
é: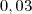
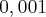
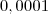
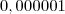

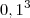 é igual a
é igual a  na quantidade de zeros, entenderam?
na quantidade de zeros, entenderam?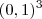 é
é 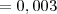 e
e  é
é 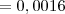 não era para ser
não era para ser  ? Porque o
? Porque o  é multiplicado
é multiplicado  vezes então era para ser
vezes então era para ser  zeros, não é? E o
zeros, não é? E o  está certo, porque
está certo, porque  é multiplicado 3 vezes, gerando 3 zeros.
é multiplicado 3 vezes, gerando 3 zeros.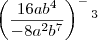

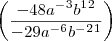

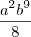
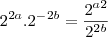 o por quê? Que o sinal do b passou para baixo positivo?
o por quê? Que o sinal do b passou para baixo positivo?