Silvanuno, bom dia... Basta você verificar, por exemplo, os três primeiros valores de ai (a1,a2,a3), para entender que a1 = -1 , e todos os demais termos a(a2,a3,a4,a5...etc), sempre resultarão em zero.(O a0 , que na verdade seria o primeiro elemento, pois i ? ?, também resultará em zero: ao = 0(zer...


 CN. Determine
CN. Determine 

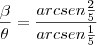
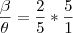 = 2
= 2