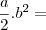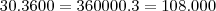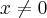Bonita questão, pega muita gente. Equação Diofantina Linear: -50.x + 33.y =83 , com X e Y naturais é claro que uma solução é {x}_{0}=-1 e {y}_{0}=1 Fórmula da Equação Diofantina Linear: X={x}_{0}+\frac{b}{d}.t e Y={y}_{0}-\frac{a}{d}.t , onde d=mdc(a,b) , a é o coeficiente de x ,b é o coeficiente de...


 = Senx
= Senx
![\frac{cateto .adjacente (o. outro. cateto)}{hipotenusa}=Cos30=\frac{\sqrt[2]{3}}{2} \frac{cateto .adjacente (o. outro. cateto)}{hipotenusa}=Cos30=\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/0cd673403c1ac06b7ccfaf43f47ae1cb.png)
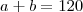
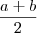
 MG temos:
MG temos:
![\sqrt[2]{a.b} \sqrt[2]{a.b}](/latexrender/pictures/b1aa488d7bbf6b51065de9b7abf15bfd.png)
 a.b
a.b máximo, temos que ter a.b máximo
máximo, temos que ter a.b máximo