Ajuda Matemática • Pesquisar

Obrigado pelas dicas ajudou bastante.

f(u,v,W) \frac{cos(u-V)-1}{1-sin(u+W)} calcular as primeiras derivadas e o seu gradiente,encontrar um ponto onde f se anule ou não. vou considerar cos(u-v) como um todo e é cos (x) ou vou ter que dizer que cos(u-v)= cosu.cosv+sinu.sinv e tambem não sei o que faço com o -1. E no denom...

Muito agredecido pela ajuda prestada já cheguei ao resultado, tambem quase que me fez o exercicio todo, sua ajuda foi preciosa, consegui entender, é conta que nunca mais acaba.

muito obrigada pela ajuda, mas realmente não chego lá e não consigo fazer as contas de derivadas, estou a tentar mas ao calcular oa variável z empacou e não vai lá, e enquanto eu não conseguir fazer as derivadas bem não vou conseguir fazer este tipo de exercicios, percebo o que se pretende e não sei...

muito obrigado pelo esclarecimento e sua disponibilidade.

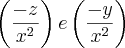pode me explicar porque não está fácil de entender para mim como fez a conta $\left(\frac{-z}{{x}^{2}} \right) e \left(\frac{-y}{{x}^{2}} \right)$ ,não consigo chegar a esse valor

No livro tenho um exemplo que refere assim, sejam A e B as váriáveis mudas associadas á função G, ou seja U= G(A;B)= G \left(\frac{z}{x}-\frac{z}{y},\frac{y}{x}-\frac{y}{z} \right) e então pela regra da cadeia temos \frac{\partial u}{\partial x}=\frac{\partial G}{\partial A}\frac{\partial A}...

\mu=G\left(\frac{z}{x}-\frac{z}{y},\frac{y}{x}-\frac{y}{x} \right) mostre, que \chi\frac{\partial u}{\partial x}+y\frac{\partial u}{\partial y}+z\frac{\partial u}{\partial z}=0 penso que tenho que achar as derivadas parciais,ou seja será que devo de achar o meu A como \left(\frac{z}{x}-...

Pesquisar

Pesquisa resultou em 8 ocorrências

Re: [derivada trignométrica]

[derivada trignométrica]

Re: [função diferencial]

Re: [função diferencial]

Re: [função diferencial]

Re: [função diferencial]

Re: [função diferencial]

[função diferencial]