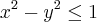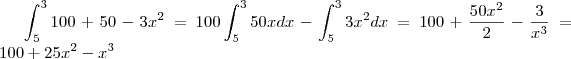Por favor analise se os limites abaixo estão corretos \lim_{\left(x,y \right)\rightarrow\left(1,1 \right)}\sqrt[]{4-{x}^{2}-{y}^{2}} \sqrt[]{4-1-1}=\sqrt[]{2}\simeq1,41 \lim_{\left(x,y \right)\rightarrow\left(1,4 \right)}5-\frac{3}{2}x+y 5-\frac{3.1}{2}+4 = 5-\frac{3}...


 essa é resposta que a professora nos passou
essa é resposta que a professora nos passou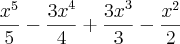


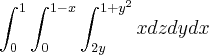

![r=\sqrt[]{{x}^{2}+{y}^{2}} r=\sqrt[]{{x}^{2}+{y}^{2}}](/latexrender/pictures/e48a93b646e01f2978a8863bd9a35b85.png) e
e 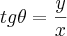

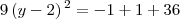
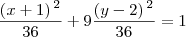
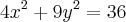
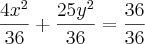
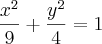

 ou não?
ou não?![f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4} f\left(x,y \right)=\sqrt[]{{x}^{2}-y+4}](/latexrender/pictures/75bd123e1e739912b46befd0bd4db182.png)


![z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{} z= \frac{\sqrt[]{25-{x}^{2}-{y}^{2}}}x{}](/latexrender/pictures/00753fe08d806fd9338e7ab3dedcf8bb.png)
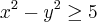
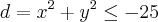
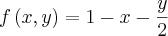
![z= \sqrt[]{\frac{x-y}{x+y}} z= \sqrt[]{\frac{x-y}{x+y}}](/latexrender/pictures/ba3aae9d1cc3593687f25a94e6f918ad.png)
![z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}} z=\frac{y}{\sqrt[]{{x}^{2}+{y}^{2}-25}}}](/latexrender/pictures/fc8349651ebe17214cf9590d0e3d8ad4.png)