Olá pessoal, poderiam me ajudar na questão a seguir: Dados os vetores u=(1, a, -2a-1), v=(a,a-1,1) e w=(a,-1,1), determinar "a" de modo que u.v=(u+v)w. Cheguei a conclusão que a=2 fazendo o seguinte: u.v=(1,a,-2a-1)(a,a-1,1)=a²-2a-1 u+v=(1+a,2a-1,-2a) (u+v)w=a²-3a+1 u.v=(u+v)w a²-2a-1=a²-3...


 Agora to vendo os de integrais, tenho prova essa semana e tô apanhando muito pra resolver...
Agora to vendo os de integrais, tenho prova essa semana e tô apanhando muito pra resolver...![\int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1 \int_{}^{}\sqrt[]{x}{sen}^{2}({x}^{\frac{3}{2}}-1)dx,
u={x}^{\frac{3}{2}}-1](/latexrender/pictures/bb89ab141a6dea0a3804327660af9aeb.png)


 ?
?
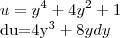



 )
)