Ajuda Matemática • Pesquisar

Supondo que o lim f(x)=L quando x->p prove que existem r>0 e M>0 tais que 0<|x-p|<r => -M <=f(x)<=M primeiramente ao analisar as afirmações, a primeira parte (0<|x-p|<r) é idêntica a definição de limite, somente empregou um r onde normalmente usamos um delta. Usando que |f(x)-L|< E (onde E é aquele ...

O exercício é o seguinte: Prove que \int\limits_{0}^{\pi}~cos^{2p+1}(x)dx=0 com p pertencente a Z. (sugestão: faça x=\pi-u ) eu tentei usar a sugestão e cai na mesma coisa de antes porém na variável u. Tentei dizer que u=senx e encontrei a seguinte integral: \int\limits_{0}^{\pi}~(1-u^2&...

hahaha, esse é um método que nenhum professor irá usar, mas dá certo. a primeira reta, se x=1, y=-10/3 logo (1, -10/3) é um ponto da reta, se x=2, y= -8/3, então (2,-8/3) é outro ponto da reta. a partir dele você pode ter um vetor diretor da reta na forma (x2-x1)i+(y2-y1)j+(z2-z1)k=v fazendo isso pa...

Eu acho que existe sim. Se você multiplicar o numerador e o denominador por 1/x e logo dizer que x=0, obterá algo do tipo 0/1 que penso eu não ser uma indeterminação

acho que faltou um sinal negativo no sen(pi.x) em baixo, mas você me ajudou MTO com essa sacada do x=u-1, muito obrigado, agora eu consegui resolver o exercício

Corrigido, obrigado !

na resolução do seguinte limite: \lim_{v\to1}\frac{1-v^2}{sen(v\pi)}} eu havia resolvido multiplicando por 1/v em cima e em baixo e encontrado 0/pi como resultado, porém depois me dei conta de que o limite fundamental trigonométrico (lim x->0 sen u / u = 1 ) somente é válido nos casos onde x...

Prove que \lim _{x \to a} x^2=a^2 Connsidere separadamente os casos em que a>0 , a<0 e a=0. (considere em sua prova 0< \epsilon <a²m quando a \ne 0 Eu consegui sem problemas fazer a demonstração com a=0, pois qualquer delta e qualquer epsilon irão permitir solucionar, então a solução fica facil... P...

O limite fornecido foi \lim _{x\to+\infty} \sqrt{x^2-5x+6}-x multipliquei em cima e em baixo por \frac{1}{x} obtendo: \lim _{x\to+\infty}x. (\sqrt{1+\frac{-5}{x}+\frac{6}{x^2}} -1) obtendo: \lim _{x\to+\infty} \infty . (\sqrt{1+ 0 + 0} -1) que dá 0. porém, o gabarito diz -5/2.. Onde ...

Muito bom luiz! muito obrigado ! Com um exercício o senhor foi capaz de esclarecer muitas dúvidas minhas !

O limite dado é o seguinte:

$\lim_{x\to0}\frac{(1+ax)^{\frac{1}{N}}-(1+bx)^{\frac{1}{N}}}{x}}$

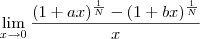
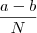sei que o resultado é $\frac{a-b}{N}$ por recorrência, afinal fiz com N=2,N=3 e N=4 e foi isso que obtive, mas não consigo partir do limite dado e chegar nessa resposta

grato pela atenção

Pesquisar

Pesquisa resultou em 11 ocorrências

[LIMITES] Limite através da definição

[Integrais] Demonstração

Re: Equação da Reta

Re: Existe ou não o limite?

Re: [limite] envolvendo funções trigonométricas

Re: [limite] envolvendo funções trigonométricas

[limite] envolvendo funções trigonométricas

[Limite] Demonstração

[limite] problema com a minha resolução

Re: [limites] calculo de limite envolvendo n e x

[limites] calculo de limite envolvendo n e x