Se bem compreendi, dado um conjunto sequêncialmente ordenado de números naturais de tamanho impar, constroi-se outro conjunto constituido pelos mesmos elementos mas com uma ordenação aleatória.Assim se C={1,2,3,4,5}, pode-se construir S={5,2,4,3,1}. Agora subtrai-se a cada termo de ordem n de C um t...


 .
.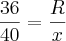 Multiplicam-se os extremos
Multiplicam-se os extremos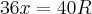 Resolve-se em ordem a x
Resolve-se em ordem a x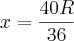 divide-se o denominador e o numerador por 4
divide-se o denominador e o numerador por 4