

 da função f(x),aplicando uma mudança de variavel
da função f(x),aplicando uma mudança de variavel  para ficar na forma mais convencional ou até olhando como
para ficar na forma mais convencional ou até olhando como  .E percebendo isto é só usar a regra do produto e avaliar no ponto
.E percebendo isto é só usar a regra do produto e avaliar no ponto 

 divisivel por
divisivel por 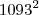 ?
? .Perceba que o termo
.Perceba que o termo  está multiplicado por 3 e que
está multiplicado por 3 e que  está multiplicado por -m.
está multiplicado por -m. .Perceba que vc ja tem o valor do produto a.b e tambem ja tem o valor da soma
.Perceba que vc ja tem o valor do produto a.b e tambem ja tem o valor da soma  .Logo você ja tem o valor de k.
.Logo você ja tem o valor de k. , o raciocínio esta no post acima.
, o raciocínio esta no post acima.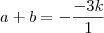 e
e 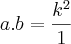 .
.![1-\sqrt[]{3}i 1-\sqrt[]{3}i](/latexrender/pictures/e92b072d503cf2e7961c2025af97f522.png) .Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.
.Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.