

![\sum_{i=1}^{\infty}\frac{1}{i\sqrt[]{i}} \sum_{i=1}^{\infty}\frac{1}{i\sqrt[]{i}}](/latexrender/pictures/2570c30153ac9110cc68ebf2d48a725b.png)
 e
e 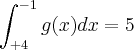 , então
, então  é:
é:

 e de
e de  . Determine r.
. Determine r.

 , resta saber as alternativas b e d
, resta saber as alternativas b e d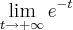 .sent[/tex]?
.sent[/tex]?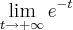 é zero, mas nao tenho certeza. nao consigo entender como seria o limite de sent
é zero, mas nao tenho certeza. nao consigo entender como seria o limite de sent onde |t|< 1 então
onde |t|< 1 então 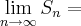 :
: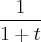 ;
; ;
; .
. , o valor médio de f(t),
, o valor médio de f(t), 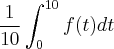 é:
é:![\int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx \int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx](/latexrender/pictures/4e5fa4eab954d480f30fc54f38ad5325.png)
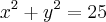 e
e 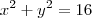 é igual a quanto? tento resolver, mas não da certo.
é igual a quanto? tento resolver, mas não da certo.