

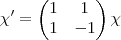
![\sqrt[]{x^2+ y^2} \leq z \leq 1 \sqrt[]{x^2+ y^2} \leq z \leq 1](/latexrender/pictures/903e7cfd27df32550b0a10149de23ab7.png) cuja densidade de massa no ponto (x; y; z) seja o quadrado da distância do ponto ao eixo z.
cuja densidade de massa no ponto (x; y; z) seja o quadrado da distância do ponto ao eixo z. 1}
1} L(V ) nos seguintes casos:
L(V ) nos seguintes casos: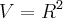 e
e 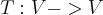 dada por
dada por  para (x,y)
para (x,y)  R^2
R^2 (x,y) por definição (x,y) != (00)
(x,y) por definição (x,y) != (00) (a,a,0) e S:
(a,a,0) e S: 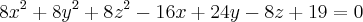 Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
Determine a para que (a) r seja tangente (b) secante (c) exterior a S. para descobrir qual é. Só consigo fazer quando é elipse mas esse dai sei que não é pois nao tem centro.
para descobrir qual é. Só consigo fazer quando é elipse mas esse dai sei que não é pois nao tem centro. . Traçar uma tangente a curva tal que a area do triangulo que ela forma com os eixos coordenados seja minima.
. Traçar uma tangente a curva tal que a area do triangulo que ela forma com os eixos coordenados seja minima.![(1+\sqrt[]{x} ) {e}^{x} tg x (1+\sqrt[]{x} ) {e}^{x} tg x](/latexrender/pictures/f7756dc64aa3a3dc5f88190eb152c9c5.png)
 uma ra?z da equação
uma ra?z da equação com a e b constantes. Se
com a e b constantes. Se 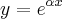 , mostre que
, mostre que
