A afirmativa no gabarito está correta... mas alguém pode me explicar porque?! - Toda dízima periódica provém da divisão de dois números inteiros, portanto é um número racional. Boom, os números 0,1 e 0,9 não são números racionais?? se 0,1/0,9 resulta em uma dízima periódica 0,111... então porque a a...



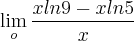

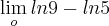
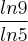


 é igual a:
é igual a: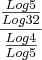



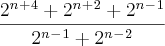
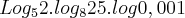

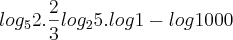
![\frac{2(-2-\sqrt[]{15})}{-4} \frac{2(-2-\sqrt[]{15})}{-4}](/latexrender/pictures/29ecaf1a9719881ecd5ec9131f450418.png)
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
![\frac{-2-\sqrt[]{15}}{2} \frac{-2-\sqrt[]{15}}{2}](/latexrender/pictures/3d75453fa63950cf33c42f3baaddc354.png)
![\frac{-4-2 \sqrt[]{15}}{-4} \frac{-4-2 \sqrt[]{15}}{-4}](/latexrender/pictures/5949a3b4548c95dc4143715439e2b24f.png)